15 Regresja liniowa
Dane są dwie zmienne losowe \(X\) i \(Y\). Załóżmy, że są one skorelowane. Możemy myśleć, że \(Y\) zależy od \(X\) (np. \((X,Y)\) to (wzrost, waga), (liczba klientów, dochód), (przebieg samochodu, zużycie paliwa), (indeks Dow Jones, indeks Wig 20)). Chcemy na podstawie obserwacji \(X(\omega_0)\) wyznaczyć \(Y(\omega_0)\). W tym celu szukamy funkcji \(f\) takiej, że \(Y = f(X)\).
Regresja liniowa polega na tym, że szuka się funkcji liniowej. Innymi słowy pracujemy przy założeniu, że zależność \(Y\) od \(X\) jest liniowa.
Przykład 15.1 Niech \(X(\omega)\) i \(Y(\omega)\) będzie budżetem filmu \(\omega\). Za zbiór zdarzeń elementarnych przyjmujemy \(\Omega\) będące zbiorem filmów (bazą internetową) zawierającą informacje o budżecie. Dla potrzeby tego przykładu posłużymy się bazą TMDB. Poniżej przedstawiamy wstępną analizę naszych zmiennych wykonaną w języku R.
# wczytujemy i czyścimy dane
movies <- read.csv("R/tmdb_5000_movies.csv")
movies_clean <- subset(movies, budget > 0 & !is.na(vote_average))
# Ustawiamy tło i kolory na wykresie
par(bg = "#002b36", col.axis = "#eee8d5", col.lab = "#eee8d5",
col.main = "#eee8d5", fg = "#eee8d5")
# Zaznaczamy punkty
plot(movies_clean$budget, movies_clean$vote_average,
main = "Ocena filmu vs budżet",
xlab = "Budżet (USD)",
ylab = "Średnia ocena",
pch = 20,
col = "#eee8d5")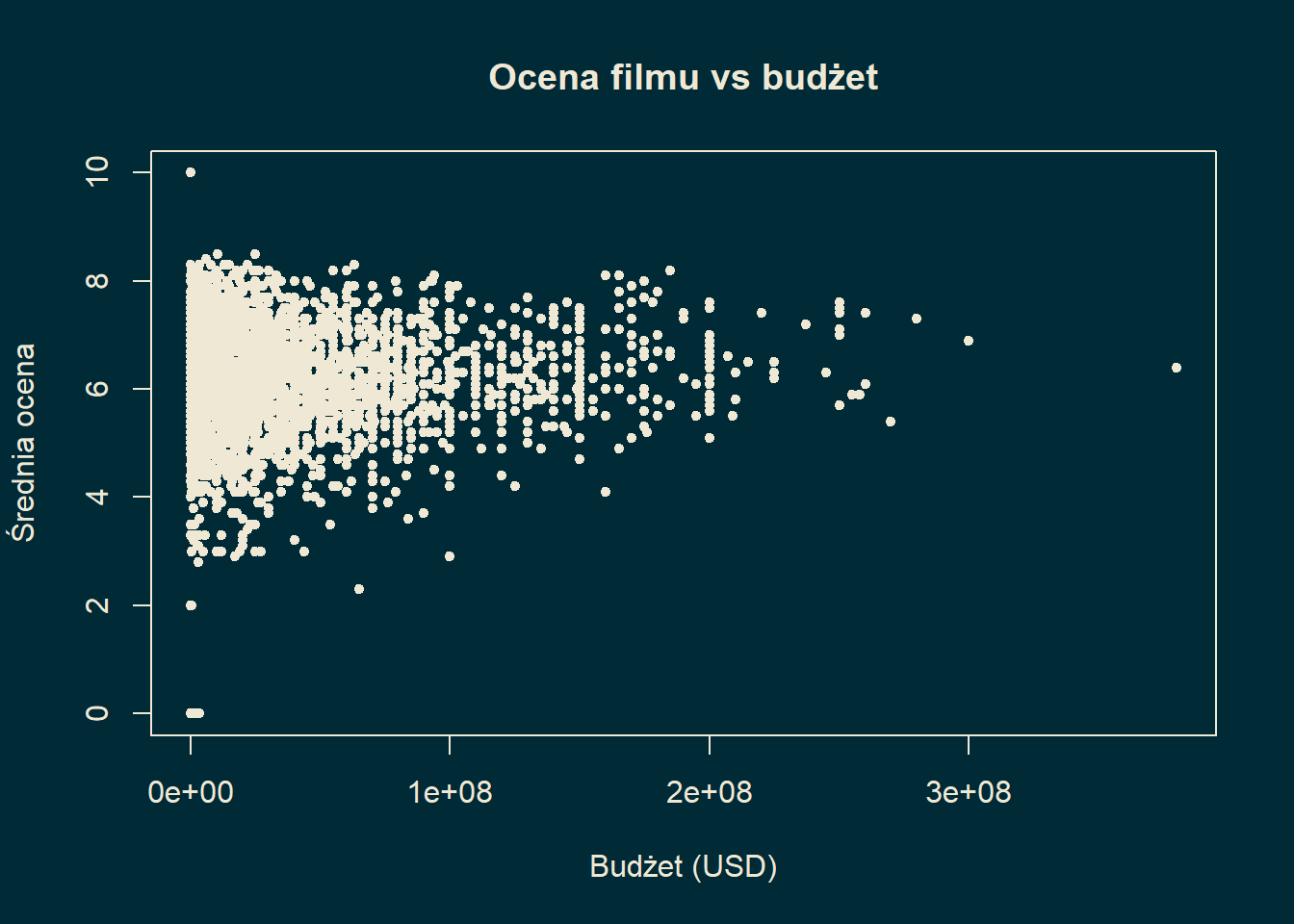
Na pierwszy rzut oka widzimy, że dane układają się symetrycznie wzdłuż osi budżetu. Sugeruje to niezależność bądź bardzo niską korelację.
Przykład 15.2 Rozważmy podobny przykład, lecz tym razem badać będziemy \(X\) będące rokiem produkcji i \(Y\) będące średnią ocen na IMBD. Za \(\Omega\) obieramy bazę 1000 najwyżej ocenianych filmów z IMDB. Należy mieć na względzie, że tutaj oceny liczone są z dokładnością do jednego miejsca po przecinku.
imdb <- read.csv("R/imdb_top_1000.csv")
imdb_clean <- subset(imdb, grepl("^[0-9]{4}$",
Released_Year) & !is.na(IMDB_Rating))
par(bg = "#002b36", col.axis = "#eee8d5", col.lab = "#eee8d5",
col.main = "#eee8d5", fg = "#eee8d5")
# Punkty
plot(imdb_clean$Released_Year, imdb_clean$IMDB_Rating,
main = "Ocena IMDb względem roku produkcji",
xlab = "Rok produkcji",
ylab = "Ocena IMDb",
pch = 20,
col = "#eee8d5")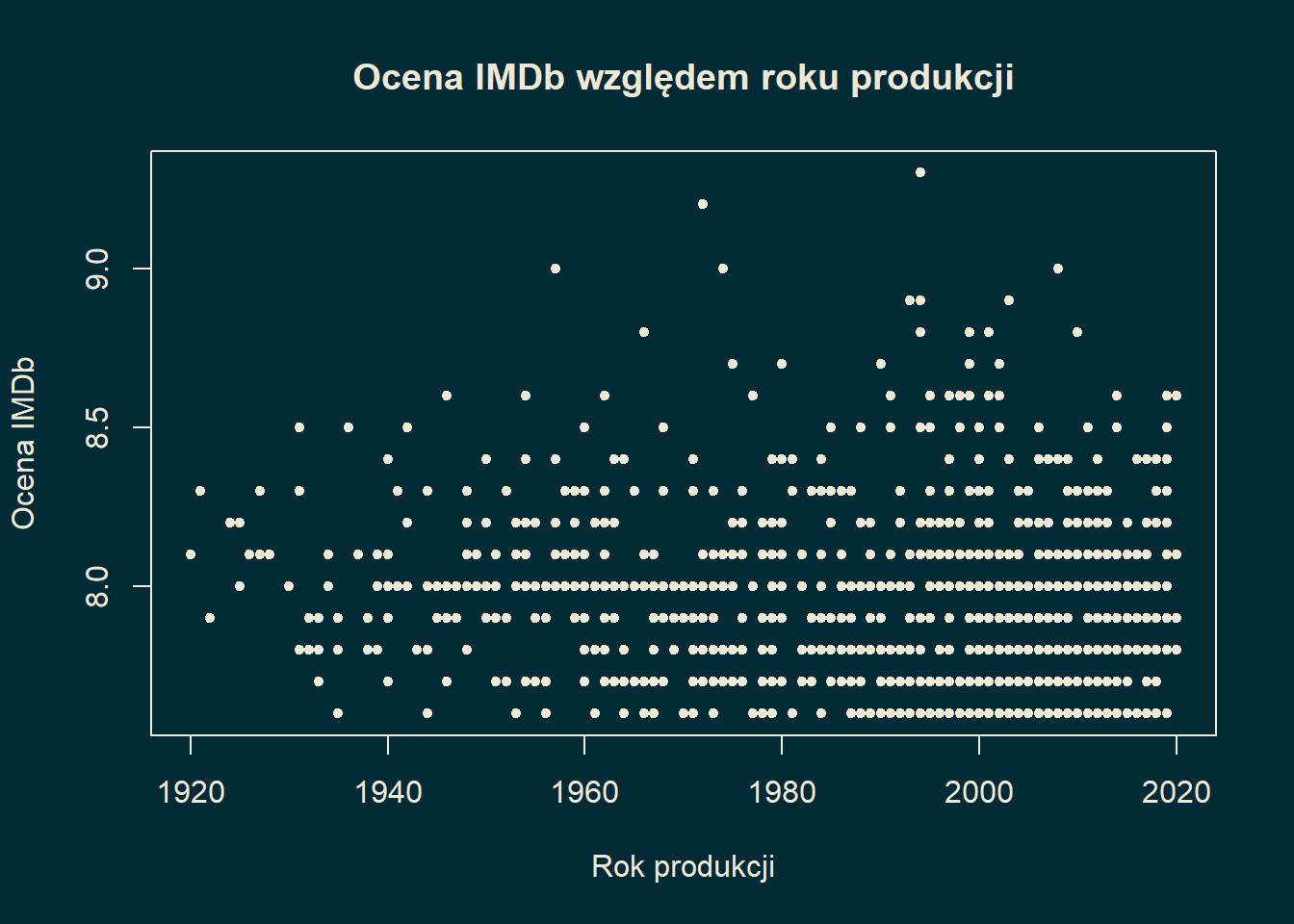
W tym przypadku widzimy tendencję spadkową.
Zanim dokończymy analizę przedstawionych wyżej przypadków omówimy problem ogólny. Będziemy chcieli wyznaczyć liniową zależność między \(X\) i \(Y\). Pytamy dla jakich wartości \(a,b \in \mathbb{R}\) zmienna \[\begin{equation*} \hat{Y} = aX+b \end{equation*}\] najlepiej przybliża \(Y\)? Błąd naszego przybliżenia będziemy liczyli w sensie średniokwadratowym Chcemy zminimalizować wartość \[ g(a,b) = \mathbb{E} \left[ \left( Y - \hat{Y} \right)^2 \right]. \] W tym celu liczymy pochodne cząstkowe i szukamy punktu, w którym zeruje się gradient \[\begin{align*} \frac{\partial g}{\partial a} & = 2a\mathbb{E}\left[ X^2 \right] - 2\mathbb{E} [XY] + 2 b \mathbb{E}[X] = 0,\\ \frac{\partial g}{\partial b} & = 2b - 2\mathbb{E}[ Y] + 2a \mathbb{E}[ X] = 0. \end{align*}\] Rozwiązując powyższy układ równań otrzymujemy \[ a = \frac{{\rm Cov}(X,Y)}{\mathbb{V}ar[ X] }, \qquad b= -\frac{{\rm Cov}(X,Y)}{\mathbb{V}ar[ X]} \mathbb{E}[ X] + \mathbb{E}[ Y]. \] Oznacza to, że szukana przez nas funkcja \(f\) ma postać \[ f(x) = y = \frac{{\rm Cov}(X,Y)}{\mathbb{V}ar[ X]}(x-\mathbb{E}[ X]) + \mathbb{E}[Y]. \] Czyli \[ \hat{Y}(\omega) = \frac{{\rm Cov}(X,Y)}{\mathbb{V}ar[ X]}(X(\omega)-\mathbb{E}[ X]) + \mathbb{E}[Y]. \] Zauważmy, że do wyznaczenia prostej regresji nie trzeba znać całego rozkładu łącznego \((X,Y)\), ale wystarczy \(\mathbb{E}[ X]\), \(\mathbb{E}[ Y]\), \(\mathbb{V}ar[ X]\), Cov\((X,Y)\). Zauważmy też, że jeżeli \(X\) i \(Y\) są dodatnio skorelowane, czyli \(\mathrm{Cov}(X,Y)>0\), to “rosnące wartości \(X\) oznaczają rosnące wartości \(Y\)’’
Przykład 15.3 Wróćmy do przykładu oceny filmu i jego budżetu. Mając nasze dane możemy obliczyć średnie, kowariancję oraz odpowiednią wariancję. Zakładamy, że wylosowanie każdego filmu jest jednakowo prawdopodobne.
# wczytujemy i czyścimy dane
movies <- read.csv("R/tmdb_5000_movies.csv")
movies_clean <- subset(movies, budget > 0 & !is.na(vote_average))
# liczymy wartości oczekiwane
Ex <- mean(movies_clean$budget)
Ey <- mean(movies_clean$vote_average)
# Kowariancja
CovXY <- sum( (movies_clean$budget - Ex) *
(movies_clean$vote_average - Ey))
# wariancja X -budżetu
VarX <- sum( (movies_clean$budget - Ex)^2 )
# liczymy współczynniki
a <- CovXY / VarX
b <- Ey - a * Ex
cat('<span style="color: #eee8d5;">Ocena = ',
b, ' + ', a, ' * budżet</span><br>')Ocena = 6.210116 + 4.41581e-10 * budżet
# Ustawiamy tło i kolory na wykresie
par(bg = "#002b36", col.axis = "#eee8d5", col.lab = "#eee8d5",
col.main = "#eee8d5", fg = "#eee8d5")
# Zaznaczamy punkty
plot(movies_clean$budget, movies_clean$vote_average,
main = "Ocena filmu vs budżet",
xlab = "Budżet (USD)",
ylab = "Średnia ocena",
pch = 20,
col = "#eee8d5")
# Prosta regresji
# Zakres budżetu (x)
x_vals <- range(movies_clean$budget)
# Odpowiednie wartości y
y_vals <- b + a * x_vals
lines(x_vals, y_vals, col = "#2aa198", lwd = 2)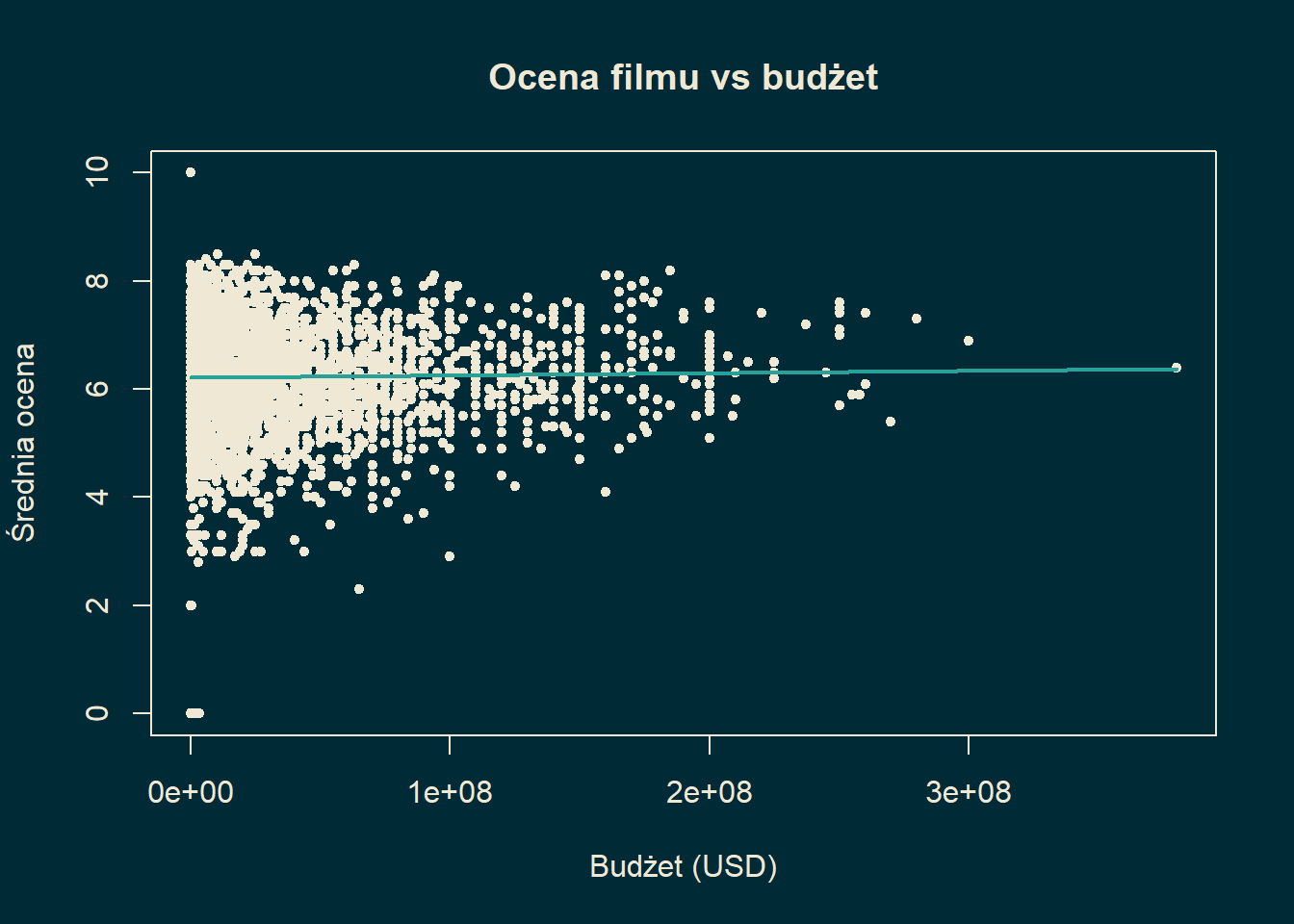
Widzimy, że w tym wypadku współczynnik korelacji jest bardzo mały. Przy tego typu wynikach nie ma statystycznej istotności: nie możemy stwierdzić, że budżet cokolwiek tłumaczy.
Przykład 15.4 Na koniec wróćmy do przykładu oceny filmu i roku produkcji.
imdb <- read.csv("R/imdb_top_1000.csv")
imdb_clean <- subset(imdb, grepl("^[0-9]{4}$",
Released_Year) & !is.na(IMDB_Rating))
imdb_clean$Released_Year <- as.numeric(imdb_clean$Released_Year)
# liczymy wartości oczekiwane
Ex <- mean(imdb_clean$Released_Year)
Ey <- mean(imdb_clean$IMDB_Rating)
# Kowariancja
CovXY <- sum( (imdb_clean$Released_Year - Ex) *
(imdb_clean$IMDB_Rating - Ey))
# wariancja X -budżetu
VarX <- sum( (imdb_clean$Released_Year - Ex)^2 )
# liczymy współczynniki
a <- CovXY / VarX
b <- Ey - a * Ex
cat('<span style="color: #eee8d5;">Ocena = ',
b, ' + ', a, ' * rok</span><br>')Ocena = 11.03454 + -0.001549247 * rok
par(bg = "#002b36", col.axis = "#eee8d5", col.lab = "#eee8d5",
col.main = "#eee8d5", fg = "#eee8d5")
# Punkty
plot(imdb_clean$Released_Year, imdb_clean$IMDB_Rating,
main = "Ocena IMDb względem roku produkcji",
xlab = "Rok produkcji",
ylab = "Ocena IMDb",
pch = 20,
col = "#eee8d5")
# Prosta regresji
# Zakres budżetu (x)
x_vals <- range(imdb_clean$Released_Year)
# Odpowiednie wartości y
y_vals <- b + a * x_vals
lines(x_vals, y_vals, col = "#2aa198", lwd = 2)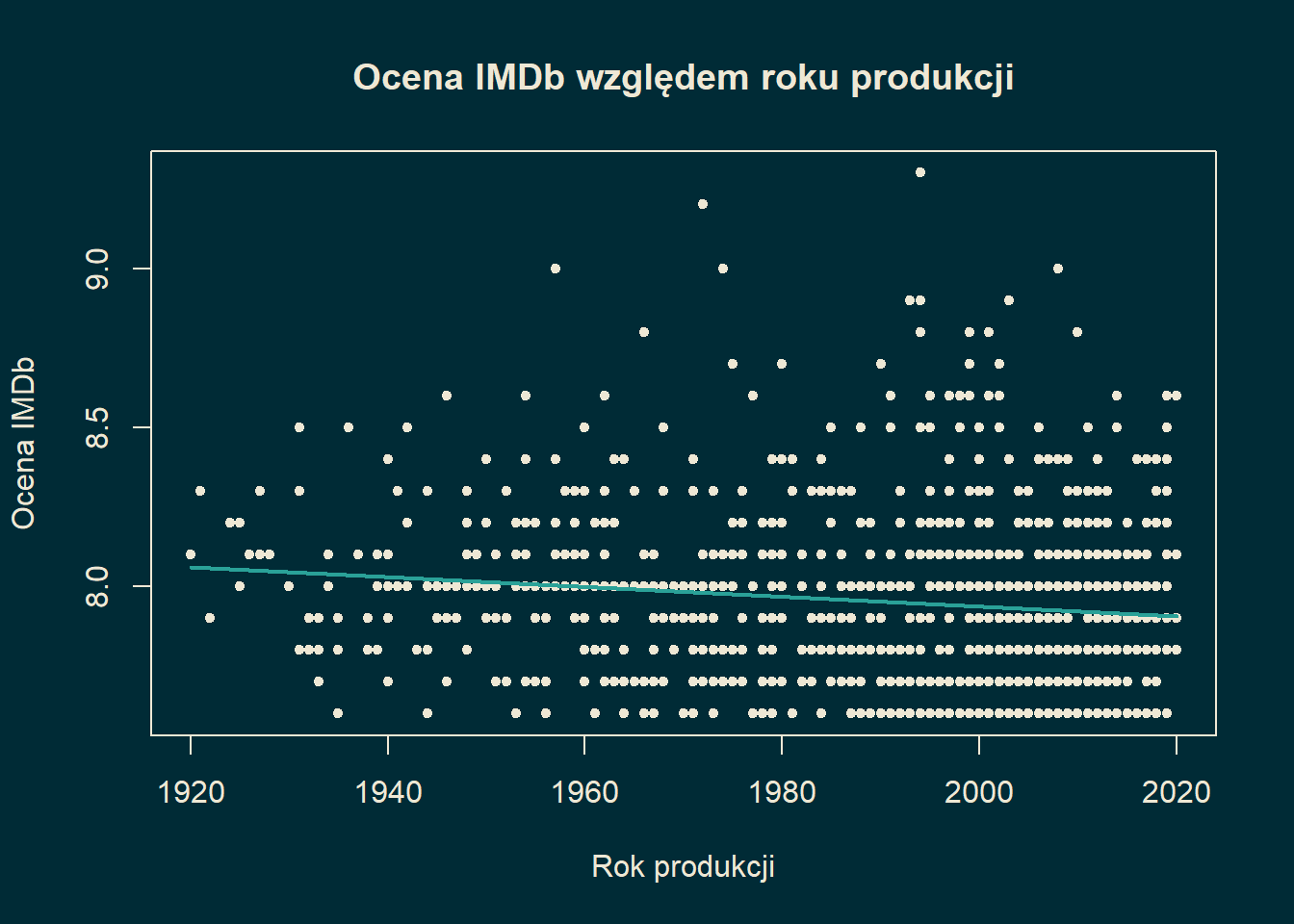
W tym przypadku widzimy, że wpływ roku jest mały (ale istotnie większy niż w przypadku budżetu!).
Przykład 15.5 Rozważmy ostatni przykład. Jak budżet filmu ma się do jego dochodów?
# wczytujemy i czyścimy dane
movies <- read.csv("R/tmdb_5000_movies.csv")
movies_clean <- subset(movies, budget > 0 & !is.na(vote_average))
# liczymy wartości oczekiwane
Ex <- mean(movies_clean$budget)
Ey <- mean(movies_clean$revenue)
# Kowariancja
CovXY <- sum( (movies_clean$budget - Ex) *
(movies_clean$revenue - Ey))
# wariancja X -budżetu
VarX <- sum( (movies_clean$budget - Ex)^2 )
# liczymy współczynniki
a <- CovXY / VarX
b <- Ey - a * Ex
cat('<span style="color: #eee8d5;">Dochody = ',
b, ' + ', a, ' * budżet</span><br>')Dochody = -5579407 + 2.956959 * budżet
# Ustawiamy tło i kolory na wykresie
par(bg = "#002b36", col.axis = "#eee8d5", col.lab = "#eee8d5",
col.main = "#eee8d5", fg = "#eee8d5")
# Zaznaczamy punkty
plot(movies_clean$budget, movies_clean$revenue,
main = "Dochody filmu vs budżet",
xlab = "Budżet (USD)",
ylab = "Dochody (USD)",
pch = 20,
col = "#eee8d5")
# Prosta regresji
# Zakres budżetu (x)
x_vals <- range(movies_clean$budget)
# Odpowiednie wartości y
y_vals <- b + a * x_vals
lines(x_vals, y_vals, col = "#2aa198", lwd = 2)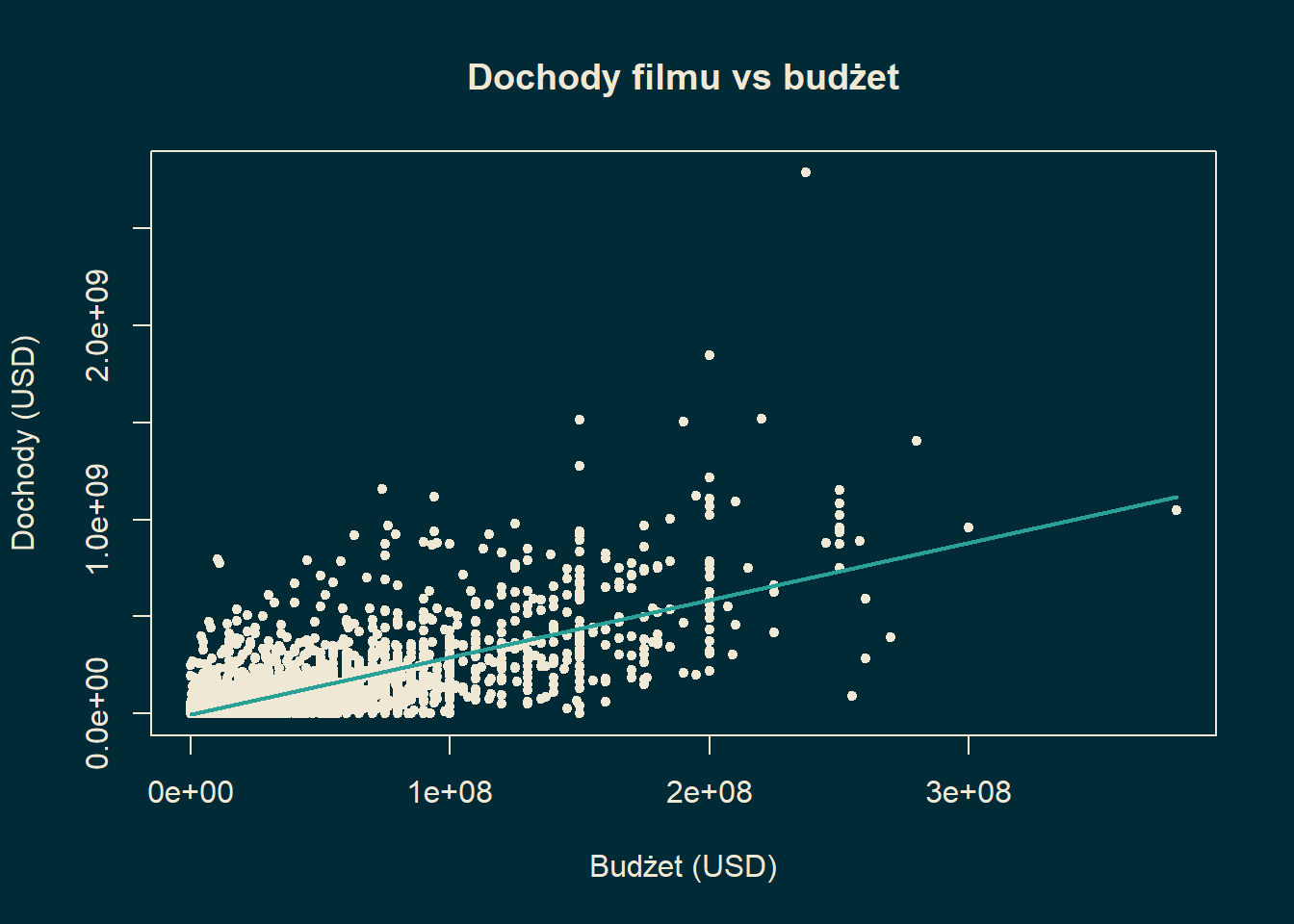
Widzimy, że w tym wypadku współczynnik korelacji jest duży.