Kontakt

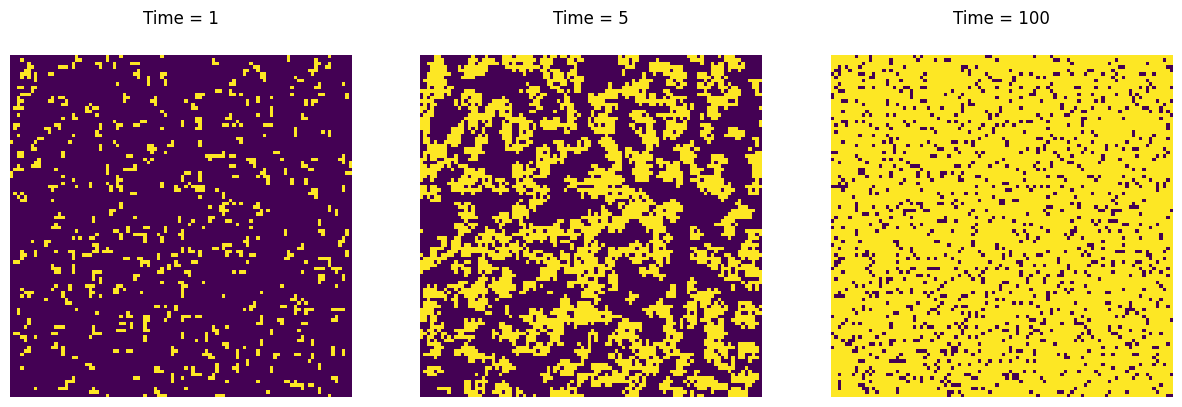
Proces ten został wprowadzony po raz pierwszy przez Harrisa (1974). Dynamika jest określona przez następujące częstości przejść: w wierzchołku \(x\), \[1 \rightarrow 0 \text{ z intensywnością } 1,\] oraz \[0 \rightarrow 1 \text{ z intensywnością } \lambda \sum_{y : |y - x| = 1} \eta(y),\] gdzie \(\lambda\) jest dodatnim parametrem, który interpretowany jest jako częstość intensywność. Miejsca, w których \(\eta(x) = 1\), są uznawane za zainfekowane, podczas gdy miejsca, w których \(\eta(x) = 0\), są uznawane za zdrowe. Zainfekowani osobnicy stają się zdrowi po czasie wykładniczym z parametrem jeden, niezależnie od konfiguracji. Zdrowi osobnicy zostają zainfekowani z częstością proporcjonalną do liczby zainfekowanych sąsiadów.