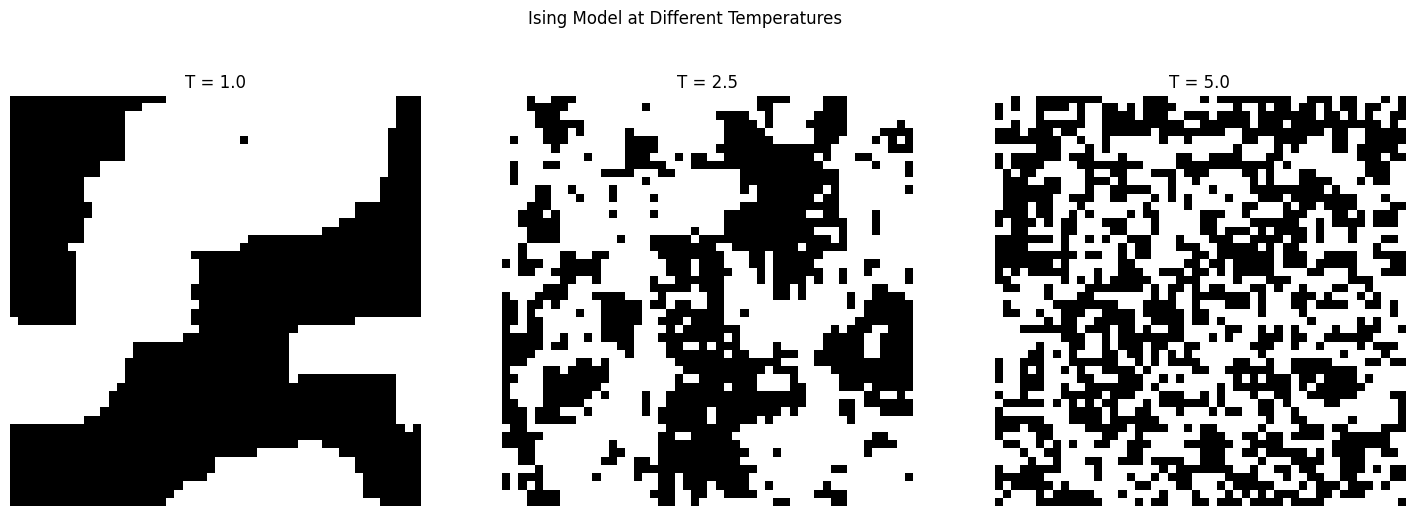
Jest to model magnetyzmu, który został wprowadzony przez Glaubera (1963) i następnie po raz pierwszy zbadany w ogólności przez Dobrushina (1971). Jest to proces z przestrzenią stanów \(\{-1, +1\}\). Wierzchołki reprezentują atomy żelaza, które są rozmieszczone na \(G\). Wartość \(\pm 1\) w wierzchołku reprezentuje spin atomu w tym wierzchołku. Dynamika jest określona przez wymóg, że spin \(\eta(x)\) w \(x \in G\) zmienia się na \(-\eta(x)\) z intensywnością \[\exp \left( -\beta \sum_{y : |y - x| = 1} \eta(y) \right),\] gdzie \(\beta=1/T\) jest nieujemnym parametrem, który reprezentuje odwrotność temperatury układu. Należy zauważyć, że częstość zmiany spinu jest wyższa, gdy spin w \(x\) różni się od większości jego sąsiadów, niż gdy jest zgodny z większością sąsiadów. Zatem układ preferuje konfiguracje, w których spiny są skoordynowane. Im większy parametr \(\beta=1/T\) tym mocniejsza jest to preferencja.

DALEJ: organizacja wykładu