Głosowanie

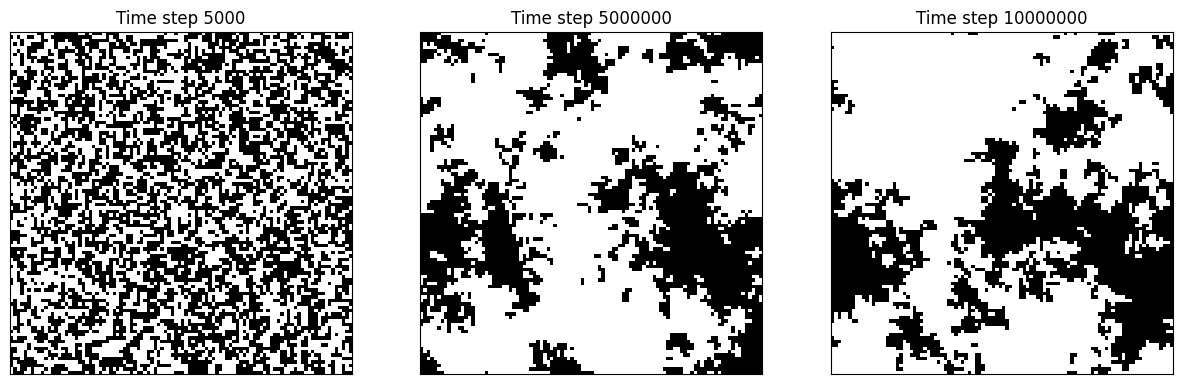
Model głosowania został wprowadzony niezależnie przez Clifforda i Sudbury’ego (1973) oraz Holley’a i Liggetta (1975). Tutaj przestrzeń stanów to \(\{0, 1\}\), a mechanizm ewolucji jest opisany w następujący sposób: \(\eta_t(x)\) zmienia się na \(1 - \eta_t(x)\) z intensywnością \[\frac{1}{\deg(x)} \sum_{y \sim x} \mathbb{1}_{\{\eta_t(y) = 1 - \eta_t(x)\}},\] gdzie \(\deg(x)\) oznacza stopień wierzchołka \(x\), \(\sum_{y \sim x}\) oznacza sumę po wszystkich sąsiadach \(x\).

W interpretacji modelu głosowania przez Holley’a i Liggetta, wierzchołki w \(G\) reprezentują wyborców, którzy mogą mieć jedno z dwóch stanowisk politycznych, oznaczanych przez zero i jeden. Wyborca czeka losowy czas wykładniczy o parametrze jeden, a następnie przyjmuje stanowisko losowo wybranego sąsiada. Clifford i Sudbury interpretują proces jako inwazję. \(\{x \in G : \eta(x) = 0\}\) i \(\{x \in G : \eta(x) = 1\}\) reprezentują terytorium zajmowane przez dwie rywalizujące populacje. Miejsce jest atakowane z intensywnością proporcjonalną do liczby sąsiednich miejsc kontrolowanych przez przeciwną populację.